

| Deutsche Version |

Fill out the gray box above and click at the calculation bar of the respective column.
Frequency means oscillations (cycles) per second in Hz = hertz = 1/s.
1 second = 1 s = 1000 ms | 1 ms = 0.001 s | 1 µs = 0.000001 s
cps = cycles per second
 |
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
Oszilloscope: Input of the boxes (Div.) and timebase (Y) give the frequency.
Formula for period (cycle duration) T
| Physical value | symbol | unit | abbreviation | formula |
| Cycle duration | T = 1 / f | second | s | T = λ / c |
| Frequency | f = 1 / T | hertz | Hz = 1/s | f = c / λ |
| Wavelength | λ | meter | m | λ = c / f |
| Wave speed | c | meter per second | m/s | c = λ × f |
| Frequency formula f = 1 / T und f = c / λ |
Time conversion - As time goes by
Formulas and equations for frequency and wavelength
| The formula for frequency is: f (frequency) = 1 / T (period). f = c / λ = wave speed c (m/s) / wavelength λ (m). The formula for time is: T (period) = 1 / f (frequency). The formula for wavelength is λ (m) = c / f λ = c / f = wave speed c (m/s) / frequency f (Hz). The unit hertz (Hz) was once called cps = cycles per second. |
| Choose: Speed of sound in air at a temperature of 20°C: c = 343 m/s or speed of radio waves and light in a vacuum: c = 299,792,458 m/s. The propagation speed of electrical signals via optical fiber is about 9/10 the speed of light, that is ≈ 270,000 km/s. The propagation speed of electrical signals via copper cables is about 2/3 the speed of light, that is ≈ 200,000 km/s. Speed of sound c = 343 m/s also equates to 1235 km/h, 767 mph, 1125 ft/s. |
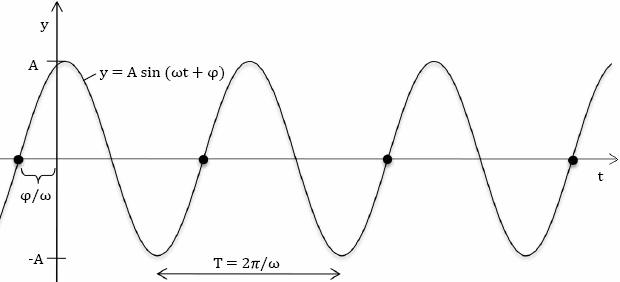 |
The Angular Frequency is ω = 2π × f
| Given is the equation: y = 50 sin (5000 t) Determine the frequency and the amplitude. Answer: The amplitude is 50 and ω = 5000. So the frequency is f = 1/T = ω / 2 π = 795.77 Hz. |
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
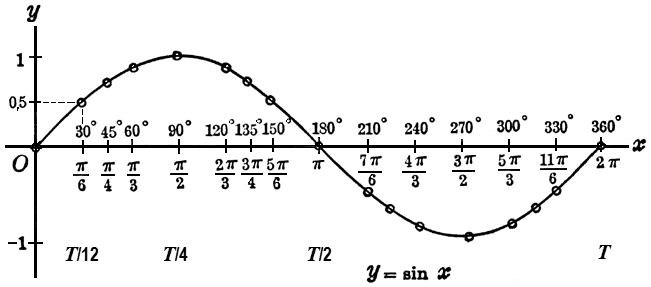
Conversion: Frequency to wavelength and vice versa
 |
| In physics and electrical engineering for the sinusoidal process is often used the angular frequency ω instead of the frequency f. The speed or frequency of revolution is a size at - preferably mechanical - rotating movements indicating the frequency of revolutions. For example, it is an essential feature for engines. It will be given in 1/min, as revolutions per minute, or as in rpm. |
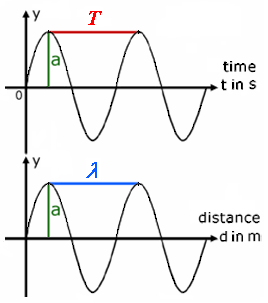 |
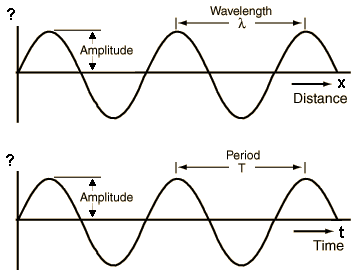
| The y axis shows the sound pressure p (sound pressure amplitude). If the graph shows at the x axis the time t, we see the period T = 1 / f. If the graph shows at the x axis the distance d, we see the wavelength λ. The largest deflection or elongation is referred to as amplitude a. |
| The amplitude has absolutely nothing to do with the frequency ... also nothing with the wavelength. |
| Waves may be graphed as a function of time or distance. A single frequency wave will appear as a sine wave (sinosoid) in either case. From the distance graph the wavelength may be determined. From the time graph, the period and frequency can be obtained. From both together, the wave speed can be determined. Source: http://hyperphysics.phy-astr.gsu.edu/hbase/sound/wavplt.html |
 |
| In acoustics an expression for a sine wave is written in the form y = A sin (2 π f T + φ). Where ω = 2 π f and A is the amplitude and where f is the frequency of the wave measured in hertz. Comparing the mathematical form y = A sin (B T + φ): With this acoustical form we see that | B | = 2 π f. Hence we have the frequency f = | B | / 2 π and the period T = 2 π / | B | = 1 / f. |
| Overtones, partials and harmonics from fundamental frequency Keyboard, frequencies = Naming of musical notes, piano keys Frequency domain of musical instruments and voices |
| SI multiples for hertz (Hz) | ||||||
| Value | Symbol | Name | Value | Symbol | Name | |
| 10−1 Hz | dHz | decihertz | 101 Hz | daHz | decahertz | |
| 10−2 Hz | cHz | centihertz | 102 Hz | hHz | hectohertz | |
| 10−3 Hz | mHz | millihertz | 103 Hz | kHz | kilohertz | |
| 10−6 Hz | µHz | microhertz | 106 Hz | MHz | megahertz | |
| 10−9 Hz | nHz | nanohertz | 109 Hz | GHz | gigahertz | |
| 10−12 Hz | pHz | picohertz | 1012 Hz | THz | terahertz | |
| 10−15 Hz | fHz | femtohertz | 1015 Hz | PHz | petahertz | |
| 10−18 Hz | aHz | attohertz | 1018 Hz | EHz | exahertz | |
| 10−21 Hz | zHz | zeptohertz | 1021 Hz | ZHz | zettahertz | |
| 10−24 Hz | yHz | yoctohertz | 1024 Hz | YHz | yottahertz | |
| Common prefixed units are in bold face. | ||||||
A typical question: What is the relationship between wavelength, temperature, and frequency?
| Explain the relationship between distance, time, and frequency in determining wavelength or: What is the equation with frequency, distance, and time? Speed = distance / time Speed = wavelength × frequency therefore Wavelength × frequency = distance / time therefore Wavelength = distance / (time × frequency) |
![]()
Masterclock calculator (clock rate)
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
![]()
Calculator with reference frequency
For downward tuning the reference frequency and piano tuning can be changed.
100 cent is equivalent to a semitone (halftone).
Note names: English and German System by comparison
Calculations of Harmonics from Fundamental Frequency
![]()
| back |
Search Engine |
home |