Quadratische Gleichung Berechnung - sengpielaudio
 
English version UK-flag - sengpielaudio D-flag - sengpielaudio
 
● Berechnung: Quadratische Gleichung ●

Die quadratischeGleichung hat in ihrer allgemeinen Form

ax^2+bx+c=0, \quad a\neq 0

die beiden Lösungen

x_{1,2} = \frac{-b\pm\sqrt{b^2-4ac}}{2a}

Die Normalform einer quadratischen Gleichung lautet

x2 + p · x + q = 0

mit reellen oder komplexen Zahlen p und q. Dabei heißen

x² = quadratisches Glied,
p · x = lineares Glied und
q = absolutes Glied der Gleichung.

Im normierten Fall, der sich durch Division beider Seiten der Gleichung durch a erreichen lässt,

x^2+px+q=0 \quad

lauten die Lösungen nach der p-q-Formel

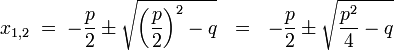
x_{1,2} \;=\; - \frac{p}{2}\pm\sqrt{ \left(\frac{p}{2}\right)^2 - q } \;\ =\;\- \frac{p}{2}\pm\sqrt{ \frac{p^2}{4} - q }

Quadratische Gleichungen haben das Format: a · x2 + b · x + c = 0

x2 + x + = 0

      


Das sind also die Werte von x1 und x2.
Der Kurvenbereich über der x-Achse ist: Quadrat-Einheiten
Die Steigung der Kurve ist an diesem Punkt:
            Der Wert der Kurve erscheint bei den Koordinaten:

Gib die Koeffizienten für die Gleichung Ax2 + Bx + C = 0 ein und der
Rechner wird die Lösungen ausgeben, wenn sie nicht imaginär sind.

Quadratische Gleichung:
Ax2 + Bx + C = 0
A = 
B = 
C = 
 
x1 =
x2 =

Wenn A = 0 ist, dann ist die Gleichung nicht quadratisch.

Beispiele für einfache Aufgaben:

Gleichung 1. Lösung 2. Lösung
x2 − 2x − 8 = 0 −2 4
2x2 + 3x − 20 = 0 −4 2,5
2x2 + 18 = 0 −9 0
x2 + 5x − 14 = 0 −7 2
3x2 + 36x − 39 = 0 −13 1
9x2 − 82x + 9 = 0 1/9 9
8x2 + 39x − 5 = 0 −5 1/8
6x2 − 12x − 6 = 0 2,414 −0,414
2,5x2 + 17,5x − 20 = 0 −8 1
49x2 + 154x + 21 = 0 −3 −1/7
4x2 + (107/3)x − 3 = 0 −9 1/12
2x2 − 20,8x + 8 = 0 2/5 10
12x2 + x − 1 = 0 −1/3 1/4
3x2 + 9x − 12 = 0 −4 1
5x2 − 2x − 3/5 = 0 −1/5 3/5
x2 − 0,9x + 0,7 = 0 −0,5 1,4
5x2 − 16,5x + 13 = 0 −2 −1,3
0,5x2 − 8x + 32 = 0 8 8

Die erste Binomische Formel:
(a + b)² = a² + 2ab + b²
Die zweite Binomische Formel:
(a − b)² = a² +2ab − b²
Die dritte Binomische Formel:
(a + b) · (a − b) = a² − b²

zurück zurück Suchmaschine weiter Startseite start