

| Deutsche Version |
| The wavelength is changing with the changing of the temperature, because the speed of sound changes with the temperature. |
|
The air pressure and the acoustic pressure p is irrelevant, when talking about the wavelength. |
| When the temperature changes, the length of the vibrating air column of a
flute or an organ pipe remains constant. Thus, when the speed of sound c
changes than also the frequency f (the pitch) changes. |
| Physical value | Symbol | Unit | Formula |
| Frequency | f = 1/T | Hz = 1/s | f = c / λ |
| Wavelength | λ | m | λ = c / f |
| Time period or cycle duration |
T = 1/f | s | T = λ / c |
| Wave speed | c | m/s | c = λ × f |
| Notice: Speed of sound in air c = 343 m/s at 20 °C (68 °F) or speed of radio waves and light in a vacuum c = 299,792,458 m/s ≈ 300,000 km/s. The propagation speed of electrical signals via optical fiber is about 9/10 the speed of light, that is ≈ 270,000 km/s. The propagation speed of electrical signals via copper cables is about 2/3 the speed of light, that is ≈ 200,000 km/s. |
| It may be worth looking how different variables act on the wave. Take the wave equation (formula): y(t) = A × (sin ω t + φ) + C The A is the amplitude and represents one half of the difference between the upper and lower peaks. The ω is the angular velocity: ω = 2 π f = 2 π / T There you find the frequency. The φ is the phase angle, the horizontal offset. The C is the vertical offset from the x-axis, usually defined as the DC offset of the waveform. "Distance = speed × time" is the key to basic wave relationship. |
| The amplitude A has nothing to do with frequency, wavelength, period of time, and speed of sound. |
Difference between speed and velocity
| Speed is a distance an object goes. Velocity is a measurement of speed and direction. Speed is a scalar quantity - it only has magnitude. Sound particle velocity is a vector quantity - it has both magnitude and direction. Speed is the first derivative of distance with respect to time. Velocity is the first derivative of displacement with respect to time. Speed and velocity are related in much the same way that distance and displacement are related. Speed is a scalar and velocity is a vector. The motion relationship "distance = velocity × time" is the key to the basic wave relationship. |
Speed of sound in different medias
| Media | Speed of sound |
| PVC soft | 80 m/s |
| Air | 343 m/s at 20°C |
| Cork | 500 m/s |
| Helium | 1 020 m/s |
| Water | 1 480 m/s |
| Polystyrol | 1 800 m/s |
| Plexiglas | 1 840 m/s |
| Concrete | 3 100 m/s |
| Tile | 3 600 m/s |
| Pine wood | 3 600 m/s |
| Granite | 3 950 m/s |
| Oak wood | 4 100 m/s |
| Iron | 5 000 m/s |
| Steel | 5 050 m/s |
| Aluminium | 5 200 m/s |
| Quartz glas | 5 400 m/s |
| Conversion of the acoustic frequency to wavelength and vice versa |
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
| Conversion of the radio frequency to wavelength and vice versa |
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
| Amplitude a, Period T and Wavelength λ |
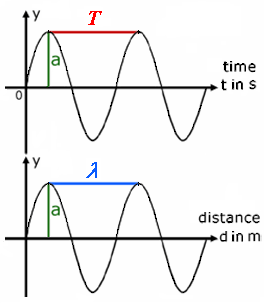 |
| y = sound pressure p (sound pressure amplitude). If the graph shows at the x axis the time t, we see the period T = 1 / f. If the graph shows at the x axis the distance d, we see the wavelength λ. The largest deflection or elongation is referred to as amplitude a. The amplitude a (strength of the wave or loudness) has nothing to do with the period, the frequency, and the wavelength. Question: "What is an amplitude?"; see: http://www.sengpielaudio.com/calculator-amplitude.htm There is not only "one" amplitude. There are many amplitudes; see: "Soundfield Quantities of a Plane Wave − Amplitudes" http://www.sengpielaudio.com/SoundfieldQuantitiesPlaneWaveAmplitude.pdf Standing waves or acoustical resonances use amplitudes; see: http://www.sengpielaudio.com/RoomModesAndStringVibrations.pdf |
A typical question: What is the relationship between wavelength, temperature and frequency?
| back |
Search Engine |
home |