

| English version |
| Der Querschnitt ist einfach eine zwei-dimensionale Sicht als Schnittdarstellung eines Objekts. Eine häufige Frage: Wie rechnet man den Durchmesser d = 2 · r (Radius) eines runden Drahts (Leiters) in den Drahtquerschnitt A oder die Querschnittsfläche A in den Drahtdurchmesser d um? Warum ist die Durchmesserangabe größer als die Flächenenangabe? Weil das nicht das gleiche ist. Die Größe eines Widerstands ist umgekehrt proportional zur Querschnittsfläche eines Leiters (Dicke). Der notwendige Querschnitt einer elektrischen Leitung ist von folgenden Einflussgrößen abhängig: 1. Nennspannung. Netzform. (Drehstrom (DS) / Wechselstrom (WS)) 2. Vorgeschaltete Sicherung = Maximal zulässiger Strom (Amp) 3. Planmäßig zu übertragende Leistung (kVA) 4. Leitungslänge in Meter (m) 5. Zulässiger Spannungfall (% von der Nennspannung) 6. Leitungsmaterial. Kupfer (Cu) oder Aluminium (Al) |
| Die "Einheit" ist üblicherweise Millimeter, kann jedoch auch Inch (Zoll) oder jedes andere Längenmaß sein, wenn bei der Fläche das Quadrat des gleichen Maßes genommen wird. |
| Klar ist, dass man auch an die Dicke der Isolierung und die Trennungsluft bei Litzen denken muss. Leitungen aus Litzen müssen wegen der aneinanderliegenden Einzeldrähte einen um etwa 14 % größeren Gesamtdurchmesser gegenüber einem Volldraht aufweisen. |
| Querschnitt ist nicht Durchmesser. |
| Der Querschnitt ist eine Fläche. Der Durchmesser ist ein Längenmaß. Das kann nicht das Gleiche sein. Der Kabeldurchmesser in Millimeter ist nicht der Kabelquerschnitt in Quadratmillimeter. |
| Der Querschnitt oder die Querschnittsfläche ist der Flächeninhalt der bei einem solchen Schnitt freigelegten Fläche. Es muss jedoch nicht unbedingt ein Kreis sein. Für Draht wird auch Kabel, Leiter oder Leitung gesagt. Handelsübliche Kabelquerschnitte: 0,75 mm2, 1,5 mm2, 2,5 mm2, 4 mm2, 6 mm2, 10 mm2, 16 mm2. |
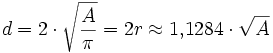
| Es gibt vier Faktoren, die den Widerstand eines Leiters beeinflussen: 1) die Querschnittsfläche A eines Leiters, berechnet aus dem Durchmesser d 2) die Länge des Leiters 3) die Temperatur, die im Leiter herrscht 4) das Material, aus dem der Leiter besteht |
| Eine genaue Formel, um den minimalen Kabelquerschnitt aus der maximalen Stromstärke zu berechnen, gibt es nicht! Das hängt von vielen Umständen ab, wie zum Beispiel, ob die Berechnung für Gleichstrom, Wechselstrom oder gar für Drehstrom sein soll, ob das Kabel frei liegt oder unter Putz gelegt ist. Auch kommt es auf die Umgebungstemperatur, die zulässige Stromdichte und den zulässigen Spannungsabfall an und ob Volldraht oder Litze vorhanden ist. Und immer gibt es den unbefriedigenden Rat der Fachleute: zur Sicherheit doch ein dickeres und damit teureres Kabel zu verwenden. Häufig tauchen Fragen nach dem Spannungsfall auf Leitungen auf. Die Spannungsabfall-Formel mit der elektrischen Leitfähigkeit κ (kappa) ist:
I = Stromstärke in Ampere l = Leitungslänge in Meter (mal 2, weil es einen Hin- und einen Rückleiter L + N gibt) κ = kappa, elektrische Leitfähigkeit (Leitwert) von Kupfer = 58 S·m/mm² (S = Siemens bei 1 m Länge und 1 mm2 Leiterfläche) κ = 1 / ρ A = Leiterquerschnittsfläche in mm2 Die Spannungsabfall-Formel mit dem spezifischem Widerstand ρ (rho) ist:
ρ = rho, spezifischer Widerstand von Kupfer = 0,01724 Ohm·mm²/m (auch Ω·m) (Ohm bei e = 1 m Drahtlänge und A = 1 mm2 Leiterfläche) ρ = 1 / κ |
|
Die abgeleitete SI-Einheit für den spezifischen Widerstand ρ ist Ω · m, gekürzt aus dem
anschaulichen Ω · mm2/m. Der Kehrwert des spezifischen Widerstands ist die elektrische Leitfähigkeit.
Elektrische Leitfähigkeit (elektr. Leitwert) κ oder σ = 1/ρ
Spezifischer Widerstand ρ = 1/κ = 1/σ
| Metallischer Leiter |
Elektrische Leitfähigkeit |
Spezifischer Widerstand |
| Silber | κ = 62 S·m/mm² | ρ = 0,0161 Ohm∙mm²/m |
| Kupfer | κ = 58 S·m/mm² | ρ = 0,0172 Ohm∙mm²/m |
| Gold | κ = 41 S·m/mm² | ρ = 0,0244 Ohm∙mm²/m |
| Aluminium | κ = 36 S·m/mm² | ρ = 0,0277 Ohm∙mm²/m |
| Konstantan | κ = 2,0 S·m/mm² | ρ = 0,5000 Ohm∙mm²/m |
Unterschied zwischen spez. Widerstand und elektr. Leitwert
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
| Der Wert der elektrischen Leitfähigkeit und des spezifischen elektrischen Widerstands ist eine temperaturabhängige Materialkonstante. Meistens wird sie bei 20 oder 25°C angegeben. |
| Bei allen Leitern ändert sich der spezifische Widerstand mit der Temperatur. Er ist in einem jeweils begrenzten Temperaturbereich näherungsweise linear: wobei α der Temperaturkoeffizient, T die Temperatur und T0 eine beliebige Temperatur, z. B. T0 = 293,15 K = 20°C, bei welcher der spezifische elektrische Widerstand ρ(T0) bekannt ist. |
Umrechnung: Widerstand in elektrischen Leitwert
Umrechnung von reziprokem Siemens in Ohm
1 Ohm [Ω] = 1 / Siemens [1/S]
1 Siemens [S] = 1 / Ohm [1/Ω]
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
1 Millisiemens = 0,001 mho = 1000 Ohm
| Mathematisch ist Konduktanz (elektrischer Leitwert) das Reziproke oder das Inverse eines Widerstands:
Einheit ist mho, d. h. "ohm" rückwärts buchstabiert. Später wurde die Einheit mho durch die Einheit Siemens ersetzt - abgekürzt mit dem Buchstaben "S". |
Tabelle für Lautsprecherkabel (Audiosignale)
| Kabel-Durchmesser d | 0,798 mm | 0,977 mm | 1,128 mm | 1,382 mm | 1,784 mm | 2,257 mm | 2,764 mm | 3,568 mm |
| Kabel-Nennquerschnitt A | 0,5 mm2 | 0,75 mm2 | 1,0 mm2 | 1,5 mm2 | 2,5 mm2 | 4,0 mm2 | 6,0 mm2 | 10,0 mm2 |
| Maximale Stromstärke | 3 A | 7,6 A | 10,4 A | 13,5 A | 18,3 A | 25 A | 32 A | - |
Wie groß muss der Leitungsquerschnitt sein?
Diese Frage hängt von mehreren Komponenten ab:
| ● von der zu übertragenden Leistung ● von der Lautsprecherimpedanz ● von der Verlegungsart des Kabels ● von der Leitungslänge |
Prinzipiell gilt: mit höherer Leistung und größerer Leitungslänge - aber auch mit geringerer Impedanz - muss der
Leitungsquerschnitt vergrößert werden. Hier ist eine Tabelle für den zu erwartenden prozentualen Leistungsverlust.
| Kabellänge in m |
Querschnitt in mm2 |
Widerstand in Ohm |
Leistungsverlust bei | Dämpfungsfaktor bei | ||
| Impedanz 8 Ohm |
Impedanz 4 Ohm |
Impedanz 8 Ohm |
Impedanz 4 Ohm |
|||
| 1 | 0,75 | 0,042 | 0,53% | 1,05% | 98 | 49 |
| 1,50 | 0,021 | 0,31% | 0,63% | 123 | 62 | |
| 2,50 | 0,013 | 0,16% | 0,33% | 151 | 75 | |
| 4,00 | 0,008 | 0,10% | 0,20% | 167 | 83 | |
| 2 | 0,75 | 0,084 | 1,06% | 2,10% | 65 | 33 |
| 1,50 | 0,042 | 0,62% | 1,26% | 85 | 43 | |
| 2,50 | 0,026 | 0,32% | 0,66% | 113 | 56 | |
| 4,00 | 0,016 | 0,20% | 0,40% | 133 | 66 | |
| 5 | 0,75 | 0,210 | 2,63% | 5,25% | 32 | 16 |
| 1,50 | 0,125 | 1,56% | 3,13% | 48 | 24 | |
| 2,50 | 0,065 | 0,81% | 1,63% | 76 | 38 | |
| 4,00 | 0,040 | 0,50% | 1,00% | 100 | 50 | |
| 10 | 0,75 | 0,420 | 5,25% | 10,50% | 17 | 9 |
| 1,50 | 0,250 | 3,13% | 6,25% | 28 | 14 | |
| 2,50 | 0,130 | 1,63% | 3,25% | 47 | 24 | |
| 4,00 | 0,080 | 1,00% | 2,00% | 67 | 33 | |
| 20 | 0,75 | 0,840 | 10,50% | 21,00% | 9 | 5 |
| 1,50 | 0,500 | 6,25% | 12,50% | 15 | 7 | |
| 2,50 | 0,260 | 3,25% | 6,50% | 27 | 13 | |
| 4,00 | 0,160 | 2,00% | 4,00% | 40 | 20 | |
Die Dämpfungsfaktor-Werte zeigen, was von einem angenommenen Dämpfungsfaktor
von 200 übrig bleibt, in Abhängigkeit von der Kabellänge, dem Kabelquerschnitt
und der Impedanz des Lautsprechers.
| Nach VDE 0100 Teil 520 = DIN 57100 Teil 520 gelten folgende Werte für den Leitungs-Mindestquerschnitt | ||
| Verlegungsart | Mindestquerschnitt in mm2 |
|
| bei Kupfer | ||
| Feste, geschützte Verlegung | 1,5 | |
| Leitungen in Schaltanlagen und Verteilern bei Stromstärken bis 2,5 A | 0,5 | |
| Über 2,5 A bis16 A | 0,75 | |
| Über 16 A | 1,0 | |
| Offene Verlegung (auf Isolatoren) Abstand der Befestigungspunkte bis zu 20 m | 4 | |
| über 20 m bis 45 m | 6 | |
| Bewegliche Leitungen für den Anschluss von leichten Handgeräten bis 1 A Stromaufnahme und einer größten Länge der Anschlussleitung von 2 m. wenn dieses in den entsprechenden Gerätebestimmungen festgelegt ist |
0,1 | |
| Geräte bis 2,5 A Stromaufnahme und einer größten Länge der Anschlussleitung von 2 m, wenn dieses in den entsprechenden Gerätebestimmungen festgelegt ist |
0,5 | |
| Geräte bis 10 A Stromaufnahme für Gerätesteck- und Kupplungsdosen bis 10 A Nennstrom | 0,75 | |
| Geräte über 10 A Stromaufnahme bei Mehrfachsteckdosen, Gerätesteckdosen und Kupplungsdosen bis 16 A Nennstrom |
1,0 | |
| Leitungen für Leistungs- und Lichtstromkreise müssen bei fester, geschützter Verlegung nach DIN 57100 Teil 520 einen Mindestquerschnitt von 1,5 mm2 Kupfer haben. |
Umrechnung von Kabeldurchmesser in AWG-Nummer
und AWG-Nummer in Durchmesser in mm
| Vorzugsweise werden Drahtstärken mit geraden Nummern verwendet, so wie 18, 16, 14, usw. Bei einem ungeraden Ergebnis, so wie 17, 19, usw., wähle die nächst niedrige gerade Nummer. AWG steht für American Wire Gauge und bezieht sich auf die Stärke von Drähten. Die AWG-Nummer gibt den Durchmesser bzw. Querschnitt eines Drahtes kodiert wieder. Generell ist diese Kabelbezeichnung nur in den USA üblich, aber gelegentlich findet man diese Angabe auch in Katalogen oder Datenblättern in Europa. |
AWG-Tabelle
| Drahtstärke AWG-Nummer |
Durchmesser (Ø) in mm |
Querschnitt in mm2 |
Drahtstärke AWG-Nummer |
Durchmesser (Ø) in mm |
Querschnitt in mm2 |
|
| 000000 (6/0) (-5) | 14,733 | 170,0 | 25 | 0,455 | 0,162 | |
| 00000 (5/0) (-4) | 13,13 | 135,0 | 26 | 0,40 | 0,125 | |
| 0000 (4/0) (-3) | 11,684 | 103,8 | 27 | 0,36 | 0,102 | |
| 000 (3/0) (-2) | 10,40 | 85,0 | 28 | 0,32 | 0,080 | |
| 00 (2/0) (-1) | 9,27 | 67,5 | 29 | 0,287 | 0,646 | |
| 0 (1/0) ( 0) | 8,25 | 53,4 | 30 | 0,254 | 0,0516 | |
| 1 | 7,34 | 42,2 | 31 | 0,226 | 0,040 | |
| 2 | 6,55 | 33,7 | 32 | 0,203 | 0,0324 | |
| 3 | 5,82 | 26,6 | 33 | 0,180 | 0,0255 | |
| 4 | 5,18 | 21,0 | 34 | 0,160 | 0,020 | |
| 5 | 4,62 | 16,9 | 35 | 0,142 | 0,0158 | |
| 6 | 4,115 | 13,25 | 36 | 0,127 | 0,0127 | |
| 7 | 3,66 | 10,25 | 37 | 0,114 | 0,010 | |
| 8 | 3,26 | 8,34 | 38 | 0,101 | 0,008 | |
| 9 | 2,90 | 6,6 | 39 | 0,089 | 0,0062 | |
| 10 | 2,59 | 5,27 | 40 | 0,079 | 0,0049 | |
| 11 | 2,30 | 4,15 | 41 | 0,071 | 0,00395 | |
| 12 | 2,05 | 3,3 | 42 | 0,064 | 0,00321 | |
| 13 | 1,83 | 2,63 | 43 | 0,056 | 0,00246 | |
| 14 | 1,63 | 2,08 | 44 | 0,050 | 0,00196 | |
| 15 | 1,45 | 1,65 | 45 | 0,0447 | 0,001569 | |
| 16 | 1,29 | 1,305 | 46 | 0,0399 | 0,001249 | |
| 17 | 1,14 | 1,01 | 47 | 0,0355 | 0,000987 | |
| 18 | 1,02 | 0,79 | 48 | 0,0316 | 0,000783 | |
| 19 | 0,91 | 0,65 | 49 | 0,0281 | 0,000621 | |
| 20 | 0,81 | 0,51 | 50 | 0,0250 | 0,000492 | |
| 21 | 0,72 | 0,407 | ||||
| 22 | 0,64 | 0,32 | ||||
| 23 | 0,57 | 0,255 | ||||
| 24 | 0,51 | 0,205 |
| Eine häufige Frage: Wie ist denn der Kabelquerschnitt zu berechnen? Querschnittsfläche A = ( I · ρ · 2 · L ) / Uv I = Maximale Stromstärke in Ampere ρ = Spezifischer Widerstand von Kupfer 0,0172 Ω mm2 / m 2·L = Benötigte Kabellänge (zweiadrig - hin und zurück) Uv = Angenommener zulässiger Spannungsverlust z. B. 0,5 V. (zulässig zwischen 3 % bis 5 %, Angabe in Volt); Uv = R · I Der Stromverbrauch ist der Quotient aus der Leistung P und der Spannung U. I = P / (U · cos φ); angenommen cos φ = 1 Ein Kabel kann nie zu dick sein - nur zu dünn. Die Verlegungsart spielt auch eine große Rolle. Erdreich? Unterputz? Manchmal wird auch mit gegebener Stromdichte gerechnet. Stromdichte J = Stromstärke I / Querschnitt A Bei gewählten 5 A/mm2 Dichte und max. 1 A wäre dann der Querschnitt (Der übliche Wert liegt bei 5 bis 6 Ampere pro mm2) Stromstärke / Dichte = 1 / 5 = 0,2 mm2 Widerstand des Kabels pro Meter: (l = Kabellänge) R = l / (58 · A) in Ohm: 58 S · m / mm² = Elektrische Leitfähigkeit von Kupfer Spannungsabfall bei 1 Ampere: U = I · R |
| zurück |
Suchmaschine |
Startseite |